Overview
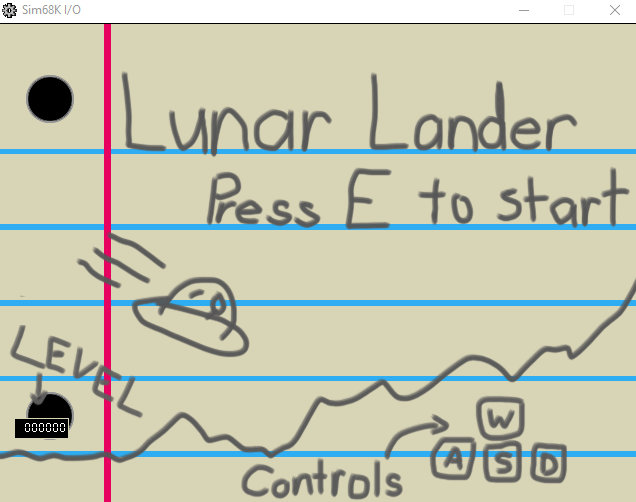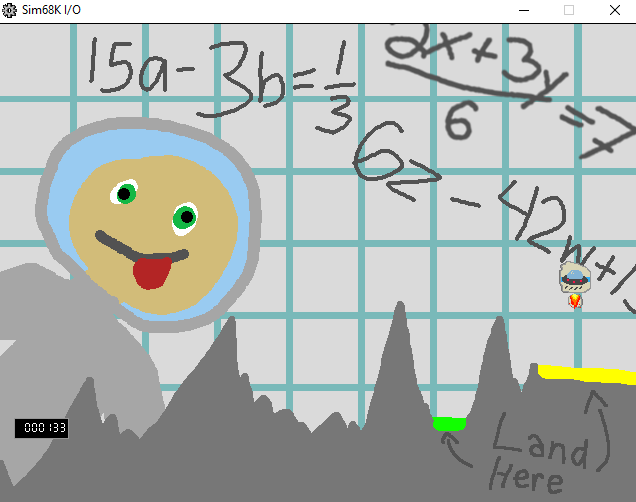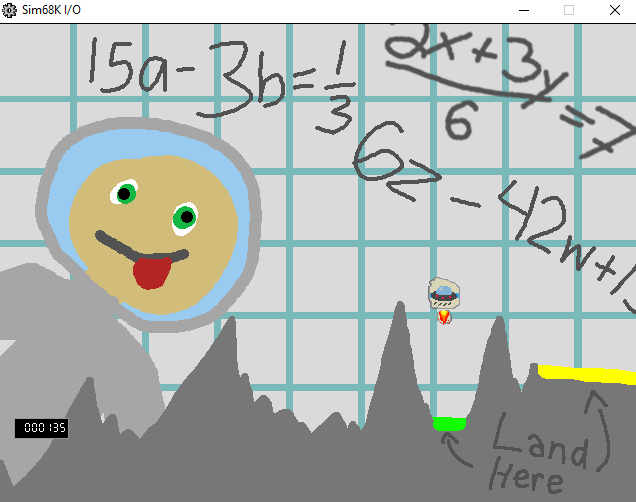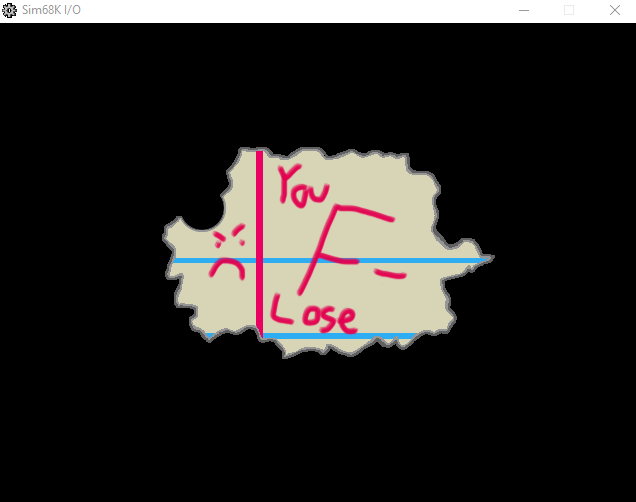
This recreation of Lunar Lander was programmed in Easy68k assembly over the course of two weeks. It features two different win conditions, physics, and a seven-segment display.
Implementation
Rendering
Rendering was accomplished by reading in a BMP file and, using its file header, extracting the necessary data to calculate the width and height of the image. From there, each individual picture was read in and drawn to the screen. As this process is costly, only the areas of the screen that had movement on top of them needed to be rewritten. This drastically sped up the program.
determineColor
* Determine color
move.l (a0), d1 ; move next color from memory into pen
* Byte shift
ror.l #8,d1 ; make sure all the bytes are in the right spots
* If color is transparent, skip it
cmp.l #TRANSPARENT_COLOR, d1
beq skipDraw
* Set color and draw pixels
move.l #PEN_COLOR_TRAP_CODE, d0 ; set the proper trap code to set the pen color
trap #15 ; set pen color through trap code
* Set location to draw
move.l d3, d1 ; x location
move.l d4, d2 ; y location
move.l #DRAW_PIXEL_TRAP_CODE, d0 ; set trap code back to drawing pixels
trap #15 ; draw pixel
skipDraw:
* Loop incrementers
addi.l #1,d3 ; increment width counter
cmp.l d3,d5 ; compare loop counter (d1) to width (d5)
bne continueRow ; continue loop
nextRow:
move.l d7, d3 ; reset width counter for next loop
subi.l #1,d4 ; decrement height counter
move.l THIS_OFFSET_Y(sp), d1
cmp.l THIS_OFFSET_Y(sp), d4 ; check if height has reached offset
bne clipX ; if it has not, continue
* Return to caller
move.l #4, d0
sub.l d0, sp
jsr loadAllRegs ; restore registers
add.l d0, sp
rts ; return from function
Physics
Physics was implemented using simple linear acceleration.
* Params: direction x, direction y
* Positive x -> right, positive y -> down
addVelocity:
* Math
* Add x direction to velocity
move.l DIR_X(sp), d0 ; move var from stack to register
cmpi.l #0, d0 ; if x velocty is 0, don't use fuel
beq skipFuelX
subi.l #1, (fuel) ; subtract 1 from fuel
skipFuelX:
muls #ACCELERATION_X, d0 ; multiply acceleration by direction to get correct direction
add.l d0, (velocityX) ; add acceleration to velocity
* Add y direction to velocity
move.l DIR_Y(sp), d0 ; move var from stack to register
muls #ACCELERATION_Y, d0 ; multiply acceleration by direction to get correct direction
cmpi.l #0, d0
beq skipFuelY
subi.l #1, (fuel) ; subtract 1 from fuel
skipFuelY:
add.l d0, (velocityY) ; add acceleration to velocityThe challenging aspect of implementing it, however, was in converting integers to floats. x86 Assembly, storing only bytes of information, does not have any inherent method to represent floats. Instead, fractional bits were used. Essentially, depending on how accurate I wanted my float to be, n fractional bits were reserved as the last n bits of the longs I used. Then, any math could be applied to those drawn out numbers, and the fractional bits can be shifted back when the number needed to be used as an integer.
* Add velocity parameters
move.l #12, d1 ; set space for parameters
sub.l d1, sp ; set up SP
move.l d5, (sp) ; move values onto stack
move.l d4, 4(sp)
jsr addVelocity
* Get x result
move.l (velocityX), d5 ; move velocity into register
add.l d5, d6 ; add it to position
* Get y result
move.l (velocityY), d5
asr.l #FRAC_BITS, d5
asr.l #FRAC_BITS, d5 ; shift d5 back
add.l d5, d7 ; add y velocity to position
add.l d1, spWin Conditions
Two win conditions and one lose condition were present in the game. The player could safely land on yellow segment for 1 point or on the green segment for 2 points. If the player had a velocity above a certain amount when they landed or landed in a different area, they would die and be sent to the start of the game. Win conditions were calculated based on the color of the pixel directly below the lunar lander. If the hex code of the color matched one of the winning colors, the player would gain a point and return to the main menu.
checkForWin:
cmpi.l #WIN, (gameWon) ; if game was not won, it was lost
bne gameEndLose
gameEndWin:
* Check for extra points
cmpi.l #1, (extraPoints)
beq showExtraPtsScreen ; if extra point win, go to extra point screen
bra showWinScreen ; if regular win, go to regular win screen
gameEndLose:
jsr redrawBackground
jsr drawSpriteBroken ; draw broken sprite if lose
jsr swapBuffer
Seven Segment Display
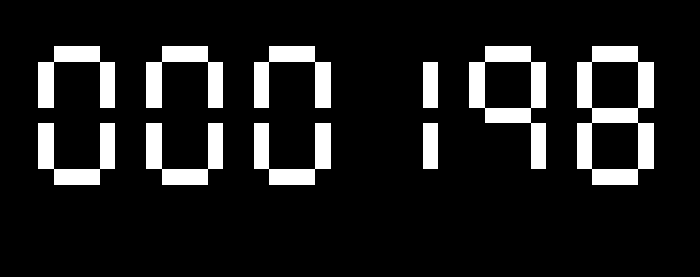
A seven segment display has one main advantage over using sprites to represent numbers: it is a lot faster. Lines being drawn instead of entire images that needed to be read in before even beginning to be drawn shaves off a ton of time. For implementing this, I stored a table to show the coordinates of every line in a single digit based around the lower left corner. Figuring out exactly how I wanted to do that took a few attempts and more than a few sketches.

segmentTable:
dc.b $3F ;0
dc.b $06 ;1
dc.b $5B ;2
dc.b $CF ;3
dc.b $66 ;4
dc.b $6D ;5
dc.b $7D ;6
dc.b $07 ;7
dc.b $7F ;8
dc.b $67 ;9
ledPositionTable
dc.l $00010003 ; a = (1,0) -> (3,0)
dc.l $01040304 ; b = (4,1) -> (4,3)
dc.l $05040704 ; c = (4,5) -> (4,7)
dc.l $08010803 ; d = (1,8) -> (3,8)
dc.l $05000700 ; e = (0,5) -> (0,7)
dc.l $03000100 ; f = (0,1) -> (0,3)
dc.l $04010403 ; g = (1,4) -> (3,4)
Once I figured out how I wanted to store each of the lines, drawing them was deceptively easy. To get each digit by itself, I used x86’s version of modulus. Then I looped through each number, and each segment of each number. After that, I used x86’s trap code for drawing a line given two coordinates.